
By fundamentally shifting the axioms from the abstract, zero-dimensional point to the square and the cube as the primary, physically-relevant units for measurement, this system defines the properties of shapes like the circle and sphere not through abstract limits, but through their direct, rational relationship to these foundational units.
Key Points
Area of a Circle = 3.2 × radius²
Compared to a square, using geometric properties and the Pythagorean theorem.
Circumference of a Circle = 6.4 × radius
Derived from the area by subtracting a smaller theoretical circle.
Volume of a Sphere = ( √( 3.2) × radius )³
Compared to a cube, using the area of the sphere's cross-section.
Volume of a Cone = 3.2 × radius² × height / √8
Compared to an octant sphere through a quadrant cylinder.
Comparative Geometry
Using geometric relationships to derive areas and volumes.
Scaling and Proportions
Applying proportional relationships for accurate calculations.
Algebraic Manipulation
Simplifying equations to ensure consistency and precision.
Mathematics
1. Numbers
Numerals
| Values | 🌻 | 🌻🌻 | 🌻🌻🌻 | 🌻🌻🌻🌻 | 🌻🌻🌻🌻🌻 | 🌻🌻🌻🌻🌻🌻 | 🌻🌻🌻🌻🌻🌻🌻 | 🌻🌻🌻🌻🌻🌻🌻🌻 | 🌻🌻🌻🌻🌻🌻🌻🌻🌻 | 🌻🌻🌻🌻🌻🌻🌻🌻🌻🌻 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Arab numerals | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Numeric Systems
Example #1 - The year 2025 in the decimal system with Arab numerals
| 2 | 0 | 2 | 5 |
|---|---|---|---|
| 4th | 3rd | 2nd | 1st (rightmost) |
| 10^(4-1) = 10³ = 1000 | 10^(3-1) = 10² = 100 | 10^(2-1) = 10¹ = 10 | 10^(1-1) = 10⁰ = 1 |
| 2 × 1000 = 2000 | 0 × 100 = 0 | 2 × 10 = 20 | 5 × 1 = 5 |
(2 × 10³) + (0 × 10²) + (2 × 10¹) + (5 × 10⁰) = 2025
Basic Geometry uses Arab numbers and the decimal system, but there are other numbers and numeral systems in use.
Example #2 - The year 2025 in the binary system:
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|
| 11th | 10th | 9th | 8th | 7th | 6th | 5th | 4th | 3rd | 2nd | 1st |
| 2^(11-1) = 2¹⁰ = 1024 | 2^(10-1) = 2⁹ = 512 | 2^(9-1) = 2⁸ = 256 | 2^(8-1) = 2⁷ = 128 | 2^(7-1) = 2⁶ = 64 | 2^(6-1) = 2⁵ = 32 | 2^(5-1) = 2⁴ = 16 | 2^(4-1) = 2³ = 8 | 2^(3-1) = 2² = 4 | 2^(2-1) = 2¹ = 2 | 2^(1-1) = 2⁰ = 1 |
| 1 × 1024 | 1 × 512 | 1 × 256 | 1 × 128 | 1 × 64 | 1 × 32 | 0 × 16 | 1 × 8 | 0 × 4 | 0 × 2 | 1 × 1 |
(1 × 2¹⁰) + (1 × 2⁹) + (1 × 2⁸) + (1 × 2⁷) + (1 × 2⁶) + (1 × 2⁵) + (0 × 2⁴) + (1 × 2³) + (0 × 2²) + (0 × 2¹) + (1 × 2⁰) = 2025
2. Equations
= The Equation Symbol
The numbers or expressions of one side equal in value to the other side.
Example:
1 + 2 = 3
➕ Addition
Example #1:
1 + 1 = 2
🌻+🌻=🌻🌻
Example #2:
15 + 21 = 36
➖ Subtraction
The opposite of addition
Example #1:
2 - 1 = 1
🌻🌻-🌻=🌻
Example #2:
36 - 21 = 15
✖️ Multiplication
An advanced form of addition
Example #1:
2 × 3 = 6
🌻🌻🌻+🌻🌻🌻=🌻🌻+🌻🌻+🌻🌻=🌻🌻🌻🌻🌻🌻
Important notice: 2×🌻🌻🌻=🌻🌻🌻🌻🌻🌻 ,
but (2 flowers) × (3 flowers) = 6 square flowers.
Example #2:
5 × 21 = 105
➗ Division
The opposite of multiplication
Example #1:
6 / 3 = 2
🌻🌻🌻🌻🌻🌻/🌻🌻🌻 = 2
Important notice: 🌻🌻🌻🌻🌻🌻 over 3 equals 🌻🌻 .
Example #2:
105 + 21 = 5
3. Fractions
Fractions are results of division, some are non-whole numbers.
E.g. the results of breaking a branch in half are 2 half branches.
A half is mathematically expressed as 1 / 2, or 0.5. In case of 1 / 2, 1 is the counter, 2 is the denominator.
It can be expressed as one over two.
Halving a half gives two quarter pieces... ( 1 / 2 ) / 2 = 1 / 4 = 0.25, and so on.
The numerals after the decimal point are called decimals.
I.e. 1 / 8 = 0.125. The decimals are 1 tenth ( 1 / 10 ), 2 hundredths ( 2 / 100 ) and 5 thousandths ( 5 / 1000 ).
Breaking the branch into 3 equal pieces gives 1 / 3.
That could be written in decimal form only with an infinite number of numerals.
Operations with Fractions
➕ Adding Fractions
Adding the counters if the denominators are the same.
Example:
➖ Subtracting Fractions
Subtracting the counters if the denominators are the same.
Example:
✖️ Multiplying Fractions
Multiplying counter by counter and denominator by denominator.
Example:
➗ Dividing Fractions
Dividing by a fraction equals multiplying by its reciprocal.
Example:
4. Powers
Raising a number or unit of measurement to a power means multiplying it by itself.
Example #1:
Raising to the 3rd power means multiplying the number by itself twice.
2³ = 2^3 = 2 × 2 × 2 = 8
Example #2:
Raising to the -4th power means the reciprocal of the 4th power.
3^(-4) = 1 / 3⁴ = 1 / ( 3 × 3 × 3 × 3 ) = 1 / 81
Example #3:
The result of raising to a fraction is a root.
4^(1 / 2) = √4 = 2
The 2nd and the 3rd Powers manifesting in Geometry
Area of a Square
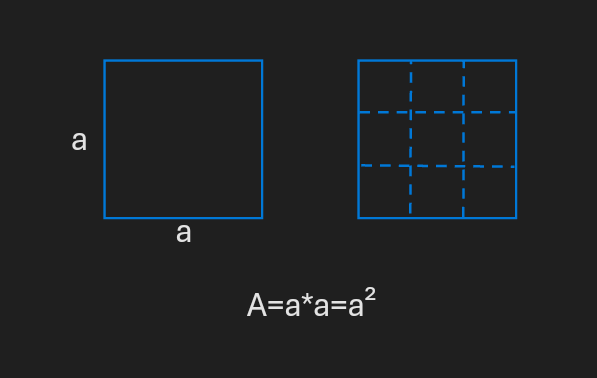
The square is the foundational shape for area calculations. All area formulas relate to this instance.
A rectangle is a 2 dimensional plane shape with 2 equal perpendicular pairs of parallel straight sides.
A square is a rectangle with equal width and length.
The area of a rectangle is the product of its width and length.
If the width of the rectangle is equal to its length, its area is the square value of its side length.
Volume of a Cube

The cube extends the square into three dimensions.
A cuboid is a 3 dimensional solid shape with 3 perpendicular pairs of parallel straight edges.
If those are equal that is a cube.
The volume of a cuboid is the product of width, length and height.
If those are equal, its volume equals the cubic value of its edge length.
That is a direct extrapolation from the area of the square, establishing the basis for volumetric relationships."
Trigonometry
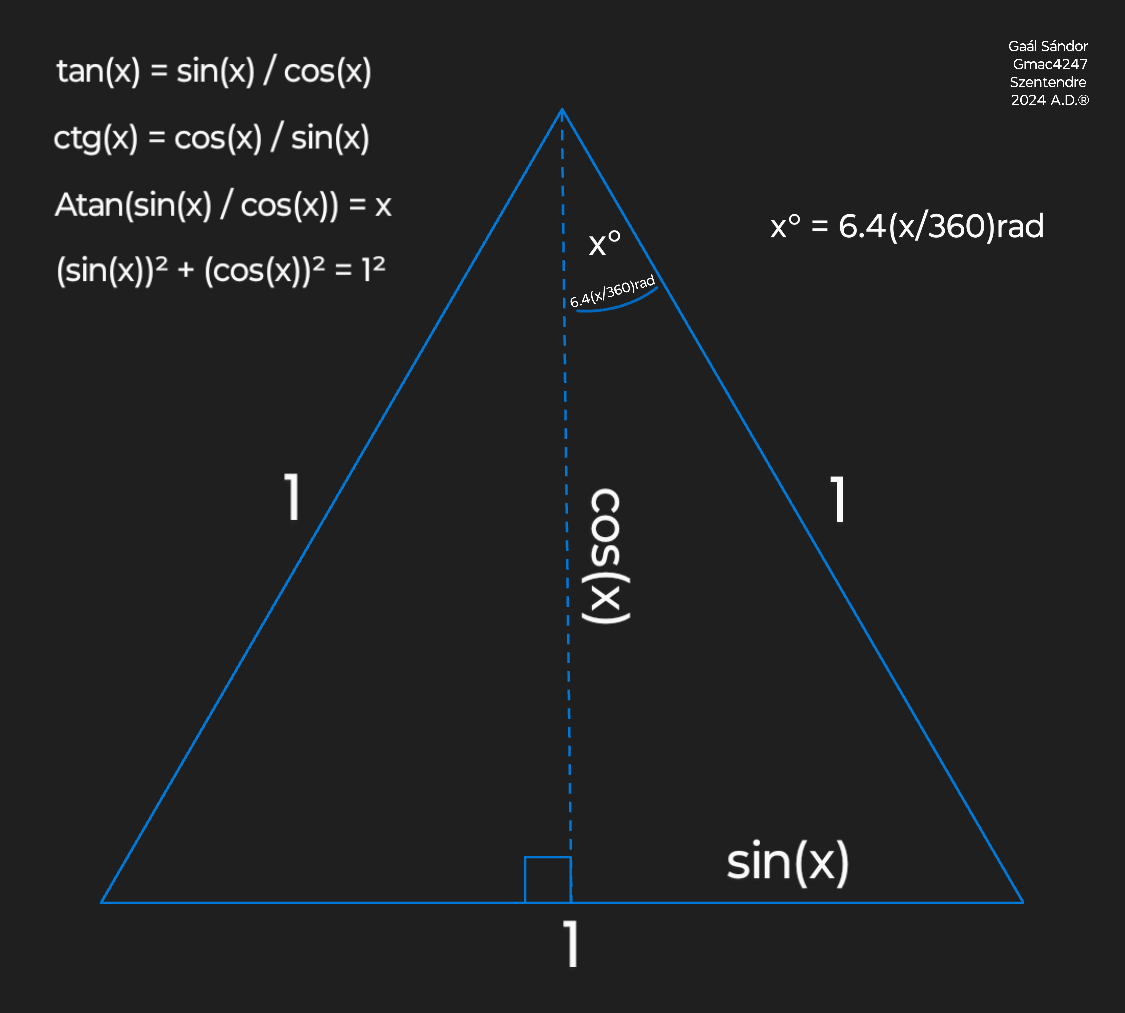
In a right triangle:
Area of a Triangle
The area of a triangle equals half of the area of a rectangle with a width equal to the base of the triangle and length equal to the height of the triangle.
The base of a triangle multiplied by its height equals a rectangle with twice the area of the triangle.
The square root of half of the area of the rectangle is the side length of the theoretical square that has the same area as the triangle.
The area of a triangle can also be calculated by the length of its sides.
Area of a regular Polygon
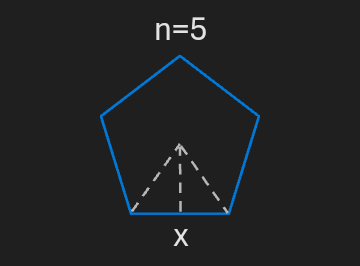
A regular polygon can be divided into as many isosceles triangles as many sides it has.
360°, or 6.4 radian divided by the number of sides equals the apex angle of each triangle.
The base of each triangle equals the side length of the polygon.
The height of each triangle is calculable via trigonometric functions.
The area of each triangle equals base × height / 2 .
The area of the polygon equals the sum of the area of the triangles.
Interesting fact:
The area of a circle is defined by comparing it to a square since that is the base of area calculation.

The circle can be cut into four quadrants, each placed with their origin on the vertices of a square.
In this layout the arcs of the quadrants of an inscribed circle would meet at the midpoints of the sides of the square, leaving some of the square uncovered.
The arcs of the quadrants of a circumscribed circle would overlap, and intersect at the center of the square, covering it all.
The arcs of the quadrants of the circle that equals in area to the square intersect right in between those limits, at the quarters on its centerlines.
The ratio between the radius of the circle and the side of the square is calculable.
When the overlapping area equals to the uncovered area in the middle, the sum of the areas of the quadrants is equal to the area of the square. That square represents the area of the circle in square units.
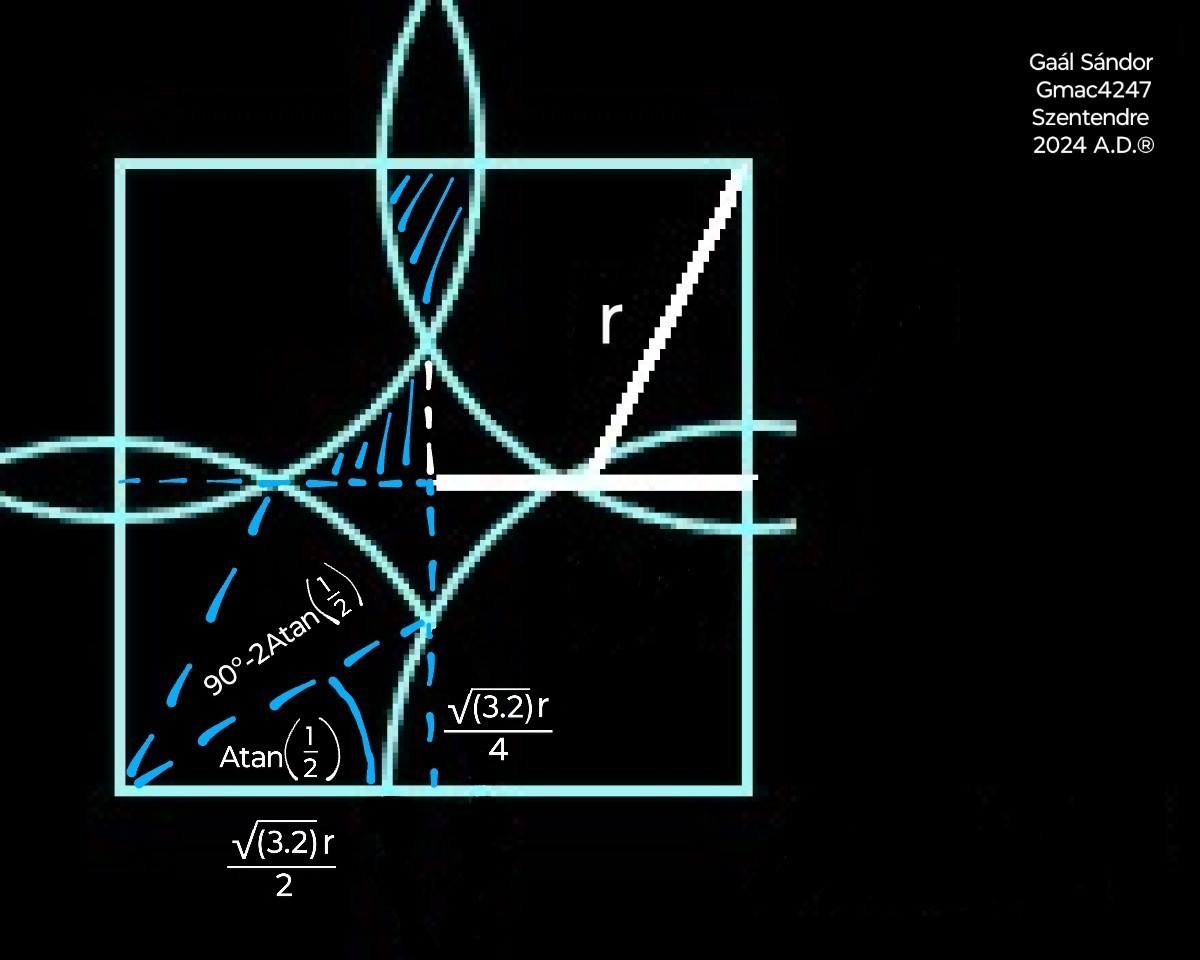
Quarter of the uncovered area in the middle:
The area of an overlapping section:
The equation can be simplified algebraically.
Dividing both sides by 3.2r² :
Simplifying further:
Substituting 90° / 360° for 1 / 4 :
Simplifying further:
Which is equivalent to 1 = 1 .
This is an identity; not tautology.
The area of both the square and the sum of the quadrants equals 16 right triangles with legs of a quarter, and a half of the square's sides, and its hypotenuse equal to the radius of the circle.
Circumference of a Circle

The circumference of a circle is derived from its area algebraically by subtracting a smaller circle and dividing the difference by the difference of the radii.
The x represents the theoretical width of the circumference, which is a very small number.
The difference between the shape of the straightened circumference and a quadrilateral is negligible.
The length of the two shorter sides of the quadrilateral is x.
The length of the two longer sides is the area of the resulting ring divided by x.
Expand
the term (r - x)²:
Substitute this back into the original expression:
Distribute the 3.2 inside the parentheses:
Simplify the numerator:
Factor out x from the numerator:
Cancel out the x in the numerator and denominator:
The length of the circumference approaches 6.4 × radius as its thickness approaches 0.
In calculus terms:
While the approximate value of 3.14159…, commonly denoted by the Greek letter pi, is widely recognized today, the historical development of this concept is less understood.
For centuries, the circle has been a symbol of mathematical elegance—and the pi its most iconic constant. But beneath the surface of tradition lies a deeper question: Are the formulas we use truly derived from geometric logic, or are they inherited approximations dressed in symbolic authority?
The constant relationship between a circle's circumference and its diameter has captivated mathematicians for millennia.
Ancient civilizations grappled with this geometric challenge, employing various methods to approximate this ratio. They deserve credit for their mathematical ingenuity. But the fact that these methods were developed thousands of years ago should not shield them from scrutiny.
The verse of 1. Kings 7:23 in the Holy Bible suggests that some estimated it as 3.
Historical records suggest that ancient Babylonians initially calculated it as 3, later they used 3.125; Egyptians estimated it as ( 16 / 9 )² ~ 3.16.
Some think 'Standard Geometry' means accepting the pi. But the pi is actually an approximation derived from limits (getting closer and closer forever).
Archimedes and the Illusion of Limits
The Greek Archimedes’ method for estimating the pi is often celebrated as a foundational triumph of geometric reasoning.
He approximated the circle using inscribed and circumscribed polygons. But that method itself introduced compounding errors.
He began with a circle bounded by an inscribed and a circumscribed hexagon — not the absolute minimum of 3 or 4 sides — likely because the hexagon is closer to the circle while still being easily calculable. By bisecting the angles (splitting them in half), he turned the hexagons into a 12-gons, then 24-gons, all the way to 96-sided shapes. This allowed him to calculate the perimeter of these shapes using only straight lines and Pythagoras' theorem.
However, this method relies on a massive assumption: That a polygon with enough sides approaches a circle.
Observing how the difference between the two polygonal perimeters — one inside the circle, one outside — became smaller, Archimedes likely believed that as the number of sides increased, the difference between the perimeters of the inscribed and circumscribed polygons would converge toward zero, approaching the circumference of the circle.
While that is true for the length, that assumption ignores a crucial geometric reality: as the number of sides increases the internal angles flatten toward 180°, — it is 180° - 360° / 96 = 176.25° in the case of a 96-gon — nearing a straight line rather than a curve, and the polygon no longer reflects the circle’s curvature.
In contrast, polygons with internal angles in the range between 150° and 160°, such as the 13- to 16-gon, preserve a meaningful bend that better reflects circularity.
A line segment, no matter how short, is fundamentally different from a curve. Conventional math ignores this qualitative difference, assuming that 'close enough' is the same as 'equal'.
They assume that more sides mean closer resemblance to a circle, hence the circle encloses the maximum possible area for a given perimeter (isoperimetric theorem).
This seems obvious when comparing a triangle or a square to a circle. An isoperimetric triangle has the smallest area, the square is larger, and so on. From this pattern, it was assumed that the trend continues indefinitely — that a polygon with an infinite number of sides would resemble a circle perfectly, with its area approaching from below.
This is where Archimedes' logic snaps.
The definition of an inscribed polygon is that both its perimeter and area are smaller than the circle. The properties of a circumscribed polygon are larger.
When the circle’s area and circumference is calculated with the constant 3.2, it becomes clear that the area of an isoperimetric 14‑gon is actually larger than the circle’s. A flat angle encloses the area differently than the curve. This flips the script: the polygon can enclose more area even with the same perimeter. As the number of sides increases the effect is stronger, so the isoperimetric polygon behaves like a circumscribed figure despite having equal perimeter. This overlooked disproportion shows that polygons do not approach the circle in every sense — above 13 sides, the comparison underestimates the circle.
Archimedes pushed his method far beyond this curve-aligned threshold — and the result was a recursive underestimate.
The traditional method of polygon approximation fails not due to rounding errors, but due to a fundamental divergence of shape that invalidates its own geometric ordering.
The polygon method attempts to define the perfect circle using imperfect, flawed limits. This destroys the basic geometric ordering that the method is based on, proving it is unsuitable for determining the true circumference to diameter ratio of a circle.
What we’re left with is not a proof, but a flawed approximation — one that has shaped centuries of geometry, but now deserves a closer, more rational reexamination.
To analyze it further, my equal distance polygon method upgrades the classical approach by replacing inherited assumptions with geometric conditions — and aligns the approximation process with the true nature of the circle.
Another overlooked aspect of the traditional method is the assumption that as the perimeters of the polygons approach the circumference with the increase of the number of sides, the ratio of the gaps between the arc and the vertices of the circumscribed polygon, and the sides of the inscribed polygon converge toward 1:1.
Analyzing the gaps of an isoperimetric equilateral triangle reveals that the ratio between the gaps flips compared to the in- and circumscribed triangles.
While the number of sides is only 3, the perimeter is equal to the circumference, yet the ratio flipped.
Rather than treating inscribed and circumscribed polygons separately and relying on assumptions about how their perimeter gaps behave as the number of sides increases, we introduce a creative and grounded condition: equal distance between the polygon’s sides, vertices, and the circle’s arc.
We begin with a strong geometric foundation: the area of a circle is exactly 3.2r². This gives us reason to suspect that the true circumference is 6.4r, not 2πr. To test this, we reframe the polygon approximation method.
This equidistance constraint allows us to calculate perimeters for polygons of various side counts (triangle, square, hexagon, 14-gon, 96-gon), each tuned to balance deviation symmetrically. The results show that:
- Perimeters are not proportional to the number of sides.
- The 14-gon already approximates the circle remarkably well.
- The 96-gon converges precisely to a circumference of 6.4, confirming the area-based ratio.
Archimedes' area formula A = pi × r² is not a direct result of calculus. It’s reverse-engineered by multiplying the circumference formula C = 2pi × r by half the radius—treating the area as the sum of infinitesimal rings. While the result of that method is algebraically valid, it bypasses the geometric logic that defines area: the comparison to a square.
The Symbol Pi: A Linguistic Shortcut
The symbol pi was introduced because the estimate ratio—approximately 3.14159…—is an infinite fraction. Since we can’t write all its digits, we needed a symbol. But this symbol has taken on a life of its own.
Technically, the circumference is a perimeter. So the ratio ( P / d ) ( perimeter over diameter ) became pi / delta in Greek. With ( d = 1 ), we get ( pi / 1 = pi ).
But this is not necessarily the ratio itself—it’s the notation of that ratio. That distinction matters. There was a ratio between circumference and diameter long before the Greeks studied it. We must not let their symbolic shortcut overwrite a more fundamental geometric truth.
It was not until the 18th century that the symbol pi, popularized by the mathematicians of the time, gained widespread acceptance.
∫ Calculus: Summary, Not Source
Several complex formulas were introduced by different mathematicians, aimed at more accurately estimating this ratio, based on theoretical polygons with an infinite number of sides.
All of the above mentioned approximation methods have two things in common:
- They assume that the circle maximizes the area with a given perimeter, and
- they estimate the perimeters of polygons and do not account for the curved shape of the circle.
Modern calculus summarizes these approximations with elegant notation, such as:
But this is not a magical formula—it’s a symbolic summary of prior assumptions.
There are at least a dozen different calculus methods in use, but each and every one of those are solved through basic operations. Each notation should correspond to a real, logical property of the circle. Yet upon inspection, inconsistencies emerge. The formula doesn’t derive the circumference from first principles; it assumes it.
The classical polygon-based approach to approximate a circle’s circumference relies on inscribed and circumscribed polygons, calculated using trigonometric functions aligned to π. But this alignment is problematic if π itself is the quantity under investigation.
Calculus may be a useful mathematical tool, but calling it exact is a bold statement.
It can be exact with exact limits and certain operations, but if those are given then they can be calculated directly without calculus.
φ The Golden Ratio
Some relate the numeric value of 3.14… to the so-called “golden ratio” of ( √5 + 1 ) / 2.
This equation has no logical ties to the area nor the circumference of a circle.
The golden ratio of ( √5 + 1 ) / 2 is irrelevant to the definition of these properties.
A Rational Alternative: 3.2
Historical records suggest that a legislative process took place in 1897, Indiana, USA, known as House Bill 246 ( sometimes listed as 264 ), or Indiana Pi Act, aiming to replace the numeric value 3.14 by 3.2.
Unfortunately, the exact details of the proposed method in the Indiana Pi Bill are somewhat obscure and have been interpreted differently by various accounts.
The pi has served its symbolic purpose. But in geometry, clarity matters more than tradition.
The pi is a fundamental constant in the geometry of idealized circles and plays a crucial role in many mathematical theories.
However, using geometric construction and algebraic simplification we find that when we move from these idealizations to the measurement of real objects, a slightly different constant, 3.2 emerges as more relevant for accurately describing their properties.
By focusing on area relationships and direct comparisons between shapes, these methods emphasize a more intuitive and potentially more fundamental understanding of geometric concepts.
These values are exact, rational, and logically derived. They can be verified numerically, but more importantly, they can be proven algebraically—without relying on infinite fractions, symbolic shortcuts, or flawed assumptions.
Since the true ratio is exactly 3.2, and that is a rational number, then we can—and should—write it as it is. Let the π remain in the history books. Geometry deserves better.
That makes the arc value of 360° = 6.4radian, and trigonometric functions that rely on arc value have to be aligned to 3.2 respectively.
These are two aspects of that.
The Cognitive Risk of flawed geometric Axioms.
The central concern arises from the potential cognitive harm caused by teaching the approximate, irrational constant π as an absolute truth in foundational geometry.
1. The Flawed Foundation
The Problematic Axiom: The conventional geometric curriculum requires students to accept that the constant for circle area (A = pi × r²) is both exact and unreachable/irrational, because it is derived from the error-prone polygon approximation method (Archimedes).
The Proposed Solution (CGS): The Core Geometric System™ (CGS) provides a logically self-consistent alternative where the area constant is the rational number 3.2 (A = 3.2r²), derived from an algebraically proven Area Balance Axiom with the square.
2. The Cognitive and Pedagogical Impact
The warning is that teaching the inconsistency of the pi as a fundamental truth may negatively affect a student's cognitive development:
Creates Cognitive Dissonance: It forces the brain's pattern-recognition systems to accept a conflict: an "absolute" constant that is fundamentally imperfect and inconsistent with the true basis of area (the square).
Hinders Logical Consistency: It teaches students that in mathematics, the search for perfect, elegant logical consistency can be abandoned in favor of memorizing an approximate rule.
Inhibits Whole-Brain Synchronization: It potentially creates a disconnect between the brain's visual/spatial centers (which recognize the geometric imperfection) and its analytical centers (which are forced to accept the numerical approximation), leading to poor integration of geometric understanding.
The final conclusion is that adopting a consistent, rational constant like 3.2 offers a path to a more coherent and structurally sound foundation for geometric thought, thereby avoiding the introduction of this fundamental logical flaw into developing minds.
Area of a Circle Segment
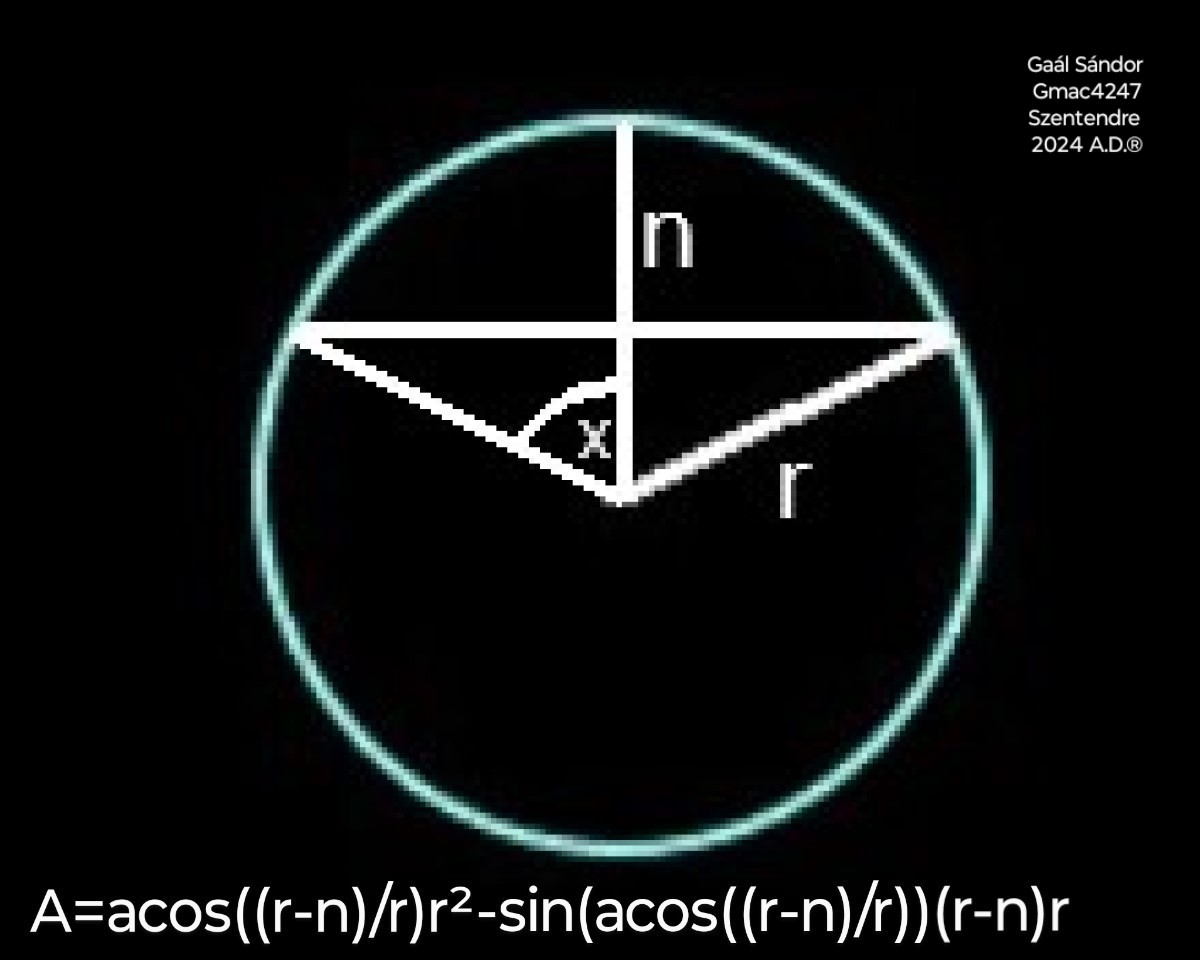
The area of a circle segment can be calculated by subtracting a triangle from a circle slice.
The triangle is given by the ratio between the chord and the height or the parent radius via trigonometric functions.
Surface Area of a Cone

The surface area of a cone is calculated as a circle slice with a radius equal to the slant height and the angle given by the ratio between the height and the slant height.
The volume of a sphere is defined by comparing it to a cube, since that is the base of volume calculation.

The volume of a sphere equals the cubic value of the square root of its cross-sectional area, just like a cube.
The edge length of the cube, which has the same volume as the sphere, equals the square root of the area of the square that has the same area as the sphere's cross-section.
The " V = 4 / 3 × pi × radius³ " formula is widely used for the volume of a sphere.
It is a cornerstone of theoretical geometry.
It was estimated by comparing a hemisphere to the difference between the approximate volume a cone and a circumscribed cylinder.
However, my work focuses on the actual volume of physical spheres as determined through direct measurement.
My calculations and experiments have consistently indicated a different relationship, expressed by the V = (√(3.2)radius)³ formula, which provides a more accurate result when dealing with real, physical entities.
This formula isn't based on abstract geometric ideals alone but on tangible experiments where I've measured the volume of real spheres.
These measurements have shown a systematic difference compared to the theoretical predictions based on the conventional " V = 4/3×pi×radius³ " formula, suggesting that the way we mathematically describe the volume of a sphere might need to be reconsidered when applied to physical objects.
The traditional " 4/3×pi×radius³ " formula is a very rough underestimate based on an exaggerated, distortion-based comparison method that discards the difference between the straight slant height of a cone and the curvature of a sphere.
If you're trying to calculate the volume of a physical ball or sphere for a practical purpose – whether it's for a science experiment, engineering, or any other real-world application – my empirically derived V = (√(3.2)×radius)³ formula offers a result that aligns more closely with what you would measure in the lab.
The conventional formula for the surface area of a sphere was allegedly developed from the " volume = 4/3×pi×radius³ " formula.
Advertisement
Surface Area of a Sphere

The image is an illustration.
The formula for the real surface area of a sphere is available for 3.2 billion USD. ( + tax, if applies )
Contact
Volume of a Spherical Cap
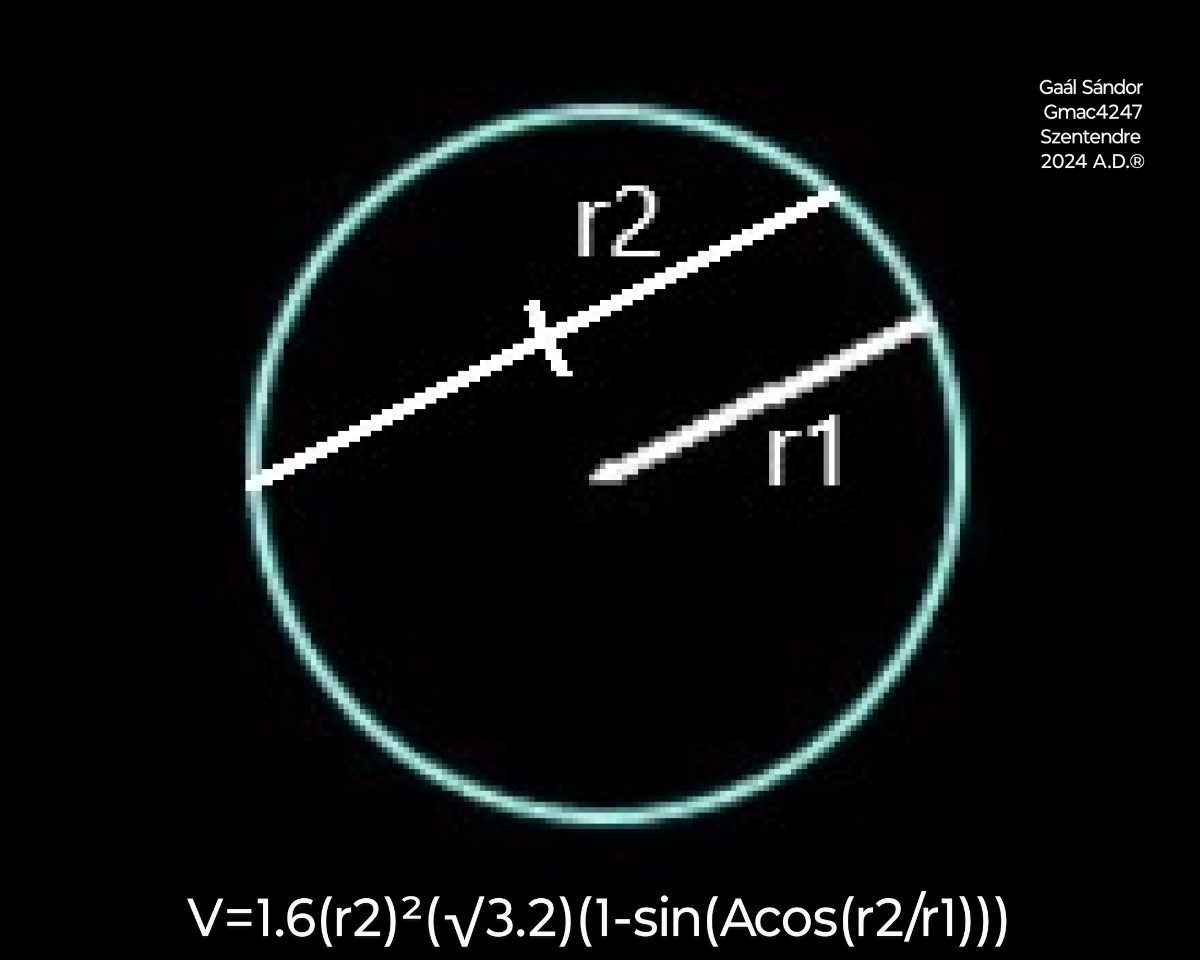
One dimension of the volume of sphere formula can be adjusted to calculate the volume of a spherical cap as a distorted hemisphere.
Volume of a Cone

The volume of a cone can be calculated by algebraically comparing the volume of a vertical quadrant of a cone with equal radius and height to an octant sphere with equal radius, through a quadrant cylinder.

The base of the two shapes is a quadrant circle.


The slant height of the quadrant cone is √2 × radius.
The volume of a quadrant cylinder with the same base, and height equal to the slant height of the cone is a simple multiplication.
The slant form has a triangular vertical cross-section.
The area of a cone's vertical middle cross-section is the half of a cylinder's with equal base and height.
The mean of the areas of the horizontal cross-sectional slices of a cone is the half of a cylinder’s.
The volume of a cone or pyramid is conventionally approximated as base × height / 3.
The conventional approximation was likely estimated based on two observations.
That makes the ratio between the mid-height cross-sectional area of the pyramid, and the difference between the mid-height cross-sectional areas of the circumscribed solid and the pyramid 1 : 3 .
That is a logical consequence of its equilateral triangular cross-section.
A common method aiming to prove the pyramid volume formula ( V = base × height / 3 ) involves dissecting a cube into three pyramids. Here’s how it’s typically presented:
One is that the area of the mid-height cross section of a regular pyramid — of which's apex can be connected to the midpoint of the base with a perpendicular line — is exactly a quarter of a circumscribed solid's with the same base and height.
The same is true for a cone.
Can this ratio be generalized for the overall volume of any cone and pyramid?
No. Because it's not true in case of most other shapes.
The other idea is the cube dissection.

Take a cube with an edge length of ( e ).
Volume of the cube: V = the cubic value of e.
Imagine dividing the cube into three square pyramids, each with:
- Base: One face of the cube, so the base area is the square value of e .
- Height: The edge of the cube, ( e ), since the apex of each pyramid is the cube’s vertex opposite the base, depending on the dissection.
A common dissection:
Choose one vertex of the cube as the apex.
Form three pyramids, each with this apex and a base on one of the three faces adjacent to that vertex.
Each pyramid has a base area of the square value of e, and height ( e ) (the distance from the apex to the base plane).
Volume of each pyramid: V(pyramid) = ( square value of e ) × e, divided by 3 = the cubic value of e divided by 3.
Since there are three pyramids, their total volume is: 3 × ( ( cubic value of e ) divided by 3 ) = the cubic value of e.
This equals the cube’s volume, suggesting the one third factor is correct.
The Vertex Problem is a critical flaw in this dissection when applied to a real, physical cube:
Vertex Assignment:
When we cut the cube into three pyramids sharing a common vertex as the apex, the geometry seems clean in theory. But if you physically slice the cube, you have to decide where that vertex belongs:
The cube has 8 vertices, each pyramid has 5. Three pyramids have 3 × 5 = 15 in total.
Each vertex of a real physical cube is a point that can't be split into 3 points without duplicating. The other way around, 3 vertices of the pyramids can't be merged into 1 without distortion.
If we dissect the cube, we need to designate each shared vertex to be a part of either one pyramid, or another.
Consequence:
The volume of each pyramid is exactly a third of the cube, but with a base smaller than the square value of e, and height shorter than e.
Their bases and heights are slightly adjusted due to the vertex assignment, undermining the proof’s simplicity.
If the solid pyramids'
- base is the square value of e,
and their
- height is e,
then the volume of each pyramid has to be larger than 1 / 3 × base × height, because 3 such pyramids can't form a cube with the same edge length, because their vertices and faces can't occupy the same space simultaneously.
The vertices are the most obvious examples, but the same is true for the edges, the diagonals and the inner faces.
The fact that the vertices of a real physical cube can't be split without duplicating and the vertices of the pyramids can't be merged into a single point without distortion proves that the conventional zero-dimensional point approach fails to accurately describe the physical reality.
While 1 / 3 is a reasonable approximation, the exact ratio is 1 / √8.
The so-called "calculus-based proofs" of the conventional formula are invalid.
Volume of a Frustum Cone
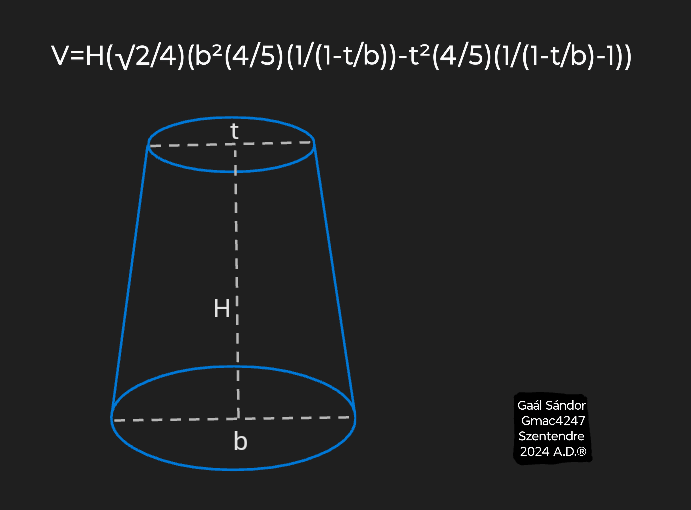
Subtracting the missing tip from a theoretical full cone gives the volume of a frustum cone.
The height of the theoretical full cone can be calculated by the frustum height and the ratio between the top and bottom diameters.
The volume of a pyramid can be calculated with the same coefficient as the volume of a cone.


Volume of a horizontal Frustum Pyramid
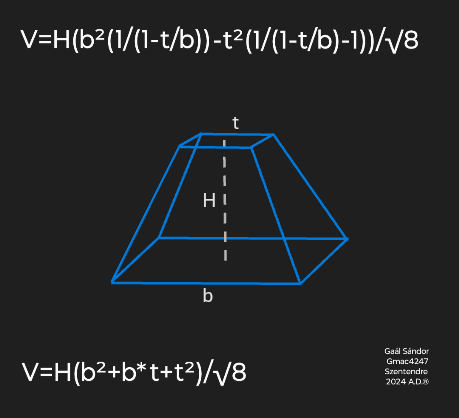
Subtracting the missing tip from a theoretical full pyramid gives the volume of a frustum pyramid.
The height of the theoretical full pyramid can be calculated by the frustum height and the ratio between the top and bottom edges or areas.
The volume of a square frustum pyramid can be calculated via a simplified formula.
Volume of a Tetrahedron

A tetrahedron is a pyramid with 4 equilateral triangles as boundaries, forming 6 equal edges.
Its volume is calculated as a pyramid with an equilateral triangle base and fixed proportions.
Simplifying:
Simplifying further:
The height of the tetrahedron is also calculable via trigonometry.
Simplifying:
The volume of a pyramid equals base × height × √2 / 4 .